线段树合并 线段树分裂 线段树优化建图(线段树三连)
线段树合并
参考资料
简介
默认使用动态开点的线段树
考虑如下问题:现在有两棵值域相同的权值线段树,你需要将两颗线段树对应节点的信息合并,得到一颗新的线段树
显然可以启发式合并做到 $O(lognlogn)$,即把叶子数小的依次插入到另一颗线段树中,在保证总点数是 $n$ 的级别下可以做到两个 $log$
由此引出一个线段树的小技巧:线段树合并
代码大概长这样
1 | func merge(a,b): |
分析下复杂度,单次合并操作的复杂度取决于两棵树公共节点(叶子)的个数,可大可小 ($O(1)$ ~ $O(nlogn)$)
假设我们有 $n$ 颗一个元素的线段树,分析下把他合并成一个的复杂度:$O(nlogn)$,因此在保证总点数的情况下复杂度是均摊 $logn$ 的
但实际用起来不一定比两个 $log$ 快。。
1 | int merge(int x,int y,int l,int r) |
例题
1. [HNOI2012]永无乡
并查集+启发式合并可以做到两个 $log$,线段树合并的话在并查集每次合并的时候($a->b,fa[b]=a$)合并根节点的线段树:$root[b]=merge(root[b],root[a])$ 即可
1 | int n,m,q; |
2. CF600E Lomsat gelral
自底向上合并线段树即可,线段树上维护每个颜色的最大出现次数和答案
比 $dsu$ 的解法快一点点
1 | GE(MAXN,MAXN*2); |
3. [Vani有约会]雨天的尾巴 /【模板】线段树合并
如果只有一种颜色,显然做一下树上差分1
s[u]++,s[v]++,s[lca]--,s[fa[lca]]--
然后自底向上合并 s[ ] 即可。
扩展到多种颜色:为每个节点 $u$ 开一个数组 $f[u][color]$,在颜色对应的位置 ++ 或 —
然后每个节点都开一个线段树来维护这个 $f[u]$ 数组,自底向上合并线段树就可以得到每个点的救济粮分发情况
在差分之后也可以沿用 $dsu$ 的解法,复杂度同样是一个 $log$,这里就练一下线段树合并啦
1 | int n,m; |
线段树分裂
线段树优化建图
依旧由一个问题来引入:[PA2011]Journeys
考虑如何实现区间连边
首先建两棵线段树 $in$ 和 $out$ ,$in$ 中父亲向儿子连边权为 $0$ 的有向边,out 中儿子向父亲连边权为 $0$ 的有向边,两颗树的叶子节点对应着由 $in$ 向 $out$ 连边权为 $0$ 的边
一个 $[1,4]$ 的例子如下:
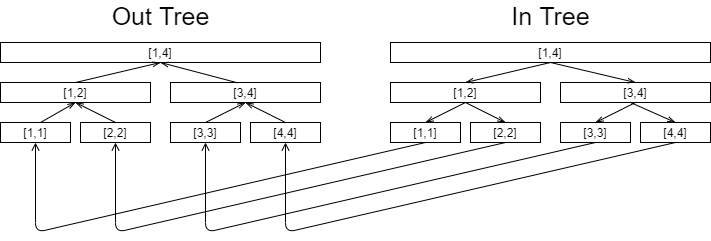
区间 $[a,b]$ 向 $[c,d]$ 连边的话,首先新建两个节点 $P1$ $P2$,$P1$ 向 $P2$ 连边权为 $1$ 的边,在 $out$ 树上找到 $[a,b]$ 对应的区间并分别向 $P1$ 连边权为 $0$ 的边,$in$ 树同理,$P2$ 分别向 $[c,d]$ 所表示的区间连边
一个 $[1,3]$ 向 $[3,4]$ 连边的例子:
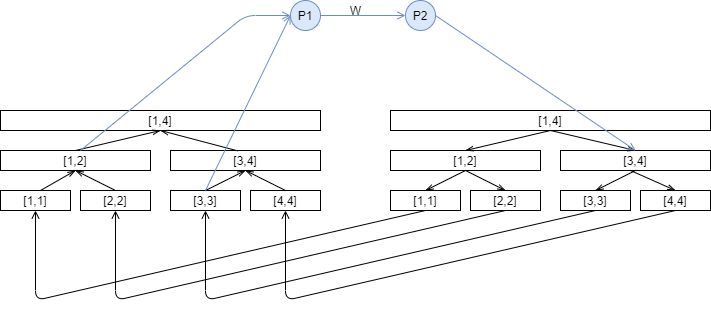
会了这个这个题就很裸了,建完图跑遍最短路即可
1 | //点数 n*4*2+m*2*2 |
线段树合并 线段树分裂 线段树优化建图(线段树三连)
http://blog.bakapiano.site/2020/05/01/线段树合并-线段树分裂-线段树优化建图-线段树三连/